Compressed Suffix Trees for Machine Translation

Matthias Petri
The University of Melbourne

joint work with Ehsan Shareghi, Gholamreza Haffari and Trevor Cohn

Machine Translation

Use computational resources to translate a sentence from a source language to a target language.

Resources

Parallel Text Corpus
- Wikipedia headlines in multiple languages
- European Parliament or UN transcripts
Large Text Corpus in the target language
Lots of data sets available for free http://www.statmt.org/wmt15/translation-task.html

Translation Process

Given a Source sentence find a translation (the Target) that has the highest probability given the source sentence:

$$P(\text{ Target }| \text{ Source }) = \frac{P(Target) \times P( \text{ Source } | \text{ Target })}{P(Source)}$$

P(Source | Target)

Find probable candidates using the Parallel Corpus

Language A	Language B	Word Alignment
lo que [X,1] que los	the [X,1] that the	0-0 1-2 3-2 4-3
lo que [X,1] que los	this [X,1] that the	0-0 3-2 4-3
lo que [X,1] que los	which [X,1] the	0-0 1-0 4-2

P(Target)

For each candidate sentence, use the text statistics of the monolingual corpus (a Language Model) to determine the "best" translation

q-gram Language Modeling

Assign a probability to a sequence of words $w^n_1$ indicating how likely the sequence is, given a language:

$$ P(w^n_1) = \prod_{i=1}^n P(w_i|w_{i-q+1}^{i-1}) $$
where $$ w^n_1 = S[1..n] \text{ and } w^j_i = S[i..j] $$

Example (q=3)

$$ P(\text{ the old night keeper keeps the keep in the town }) = \\ P(\text{ the} ) \\ \times P(\text{ old }|\text{ the }) \\ \times P(\text{ night }|\text{ the old }) \\ \times P(\text{ keeper }|\text{ the old night }) \\ \times P(\text{ keeps }|\text{ old night keeper }) \\ \times P(\text{ the }|\text{ night keeper keeps }) \\ \times P(\text{ keep }|\text{ keeper keeps the }) \\ \times P(\text{ in }|\text{ keeps the keep }) \\ \times P(\text{ the }|\text{ the keep in }) \\ \times P(\text{ town }|\text{ keep in the }) \\ $$

Kneser-Ney Language Modeling

Highest Level:

$$ P(w_i|w_{i-q+1}^{i-1})=\frac{max(C(w_{i-q+1}^i))−D_q,0)}{C(w_{i-q+1}^{i-1})} + \frac{D_q N_{1+}(w_{i-q+1}^{i-1} \bullet )}{C(w_{i-q+1}^{i-1})} P(w_i|w_{i-n+2}^{i-1}) $$

Middle Level ($1 < k < q$):

$$ P(w_i|w_{i-k+1}^{i-1})=\frac{max(N_{1+}(\bullet w_{i-k+1}^i))−D_k,0)}{N_{1+}(\bullet w_{i-k+1}^{i-1}\bullet)} + \frac{D_k N_{1+}(w_{i-k+1}^{i-1} \bullet )}{N_{1+}(\bullet w_{i-k+1}^{i-1}\bullet)} P(w_i|w_{i-k+2}^{i-1}) $$

Lowest Level:

$$ P(w_i) = \frac{N_{1+}(\bullet w_{i})}{N_{1+}(\bullet \bullet)} $$

Terminology

$C(w_{i}^j)$: Standard count of $S[i..j]$ in the corpus
$N_{1+}(\bullet \alpha) = |\{w: c(w \alpha)>0\}|$ is the number of observed word types preceding the pattern $\alpha = w_{i}^j$
$N_{1+}(\alpha \bullet ) = |\{w: c(\alpha w)>0\}|$ is the number of observed word types following the pattern $\alpha$
$N_{1+}(\bullet \alpha \bullet)$: the number of unique contexts (left and right) where $\alpha $ occurs
$D_i$: Discount parameter for the recursion computed at index construction time
$N_{1+}(\bullet \bullet)$: Number of unique bi-grams

$N_{1}(\alpha \bullet) = |\{w: c(\alpha w)==1\}|$ is the number of observed word types preceding the pattern $\alpha = w_{i}^j$ that occur exactly once
$N_{2}(\alpha \bullet) = |\{w: c(\alpha w)==2\}|$ is the number of observed word types preceding the pattern $\alpha = w_{i}^j$ that occur exactly two times
$N_{3+}(\alpha \bullet ) = |\{w: c(\alpha w)\geq3\}|$ is the number of observed word types following the pattern $\alpha$ that occur at least 3 times

ARPA Files

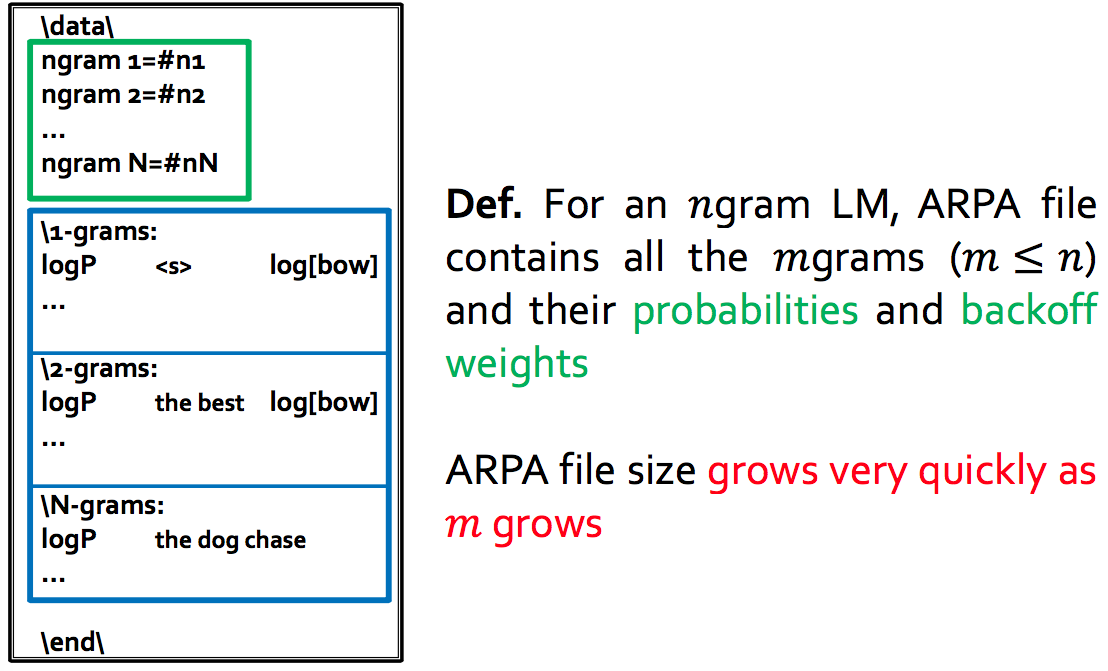
ARPA based Language Models

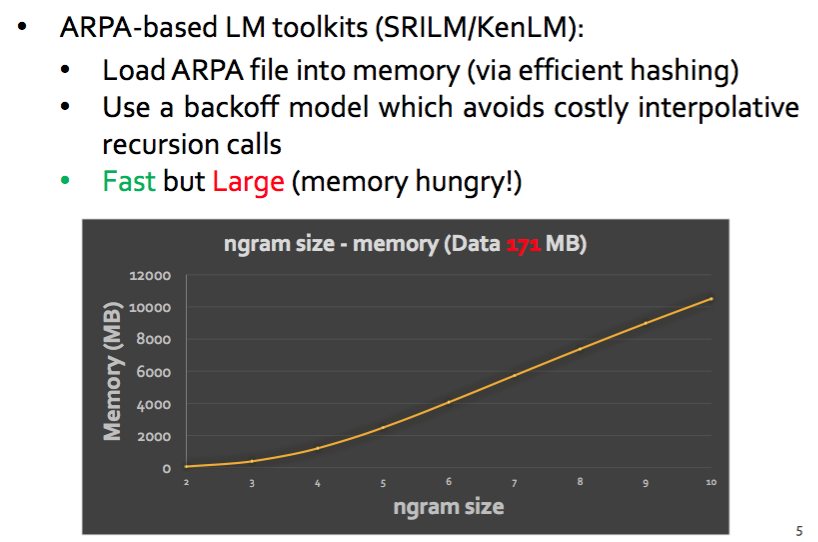
Instead of precomputation can we compute probabilities on the fly using Compressed Suffix Trees?

Advantages

No restriction in recursion depth results in better probability estimates
Current approaches prestore probabilities which uses space exponential in q
Construction of a CST is faster than precomputing all probabilities
Can operate on words and character alphabets (need larger q to be useful)

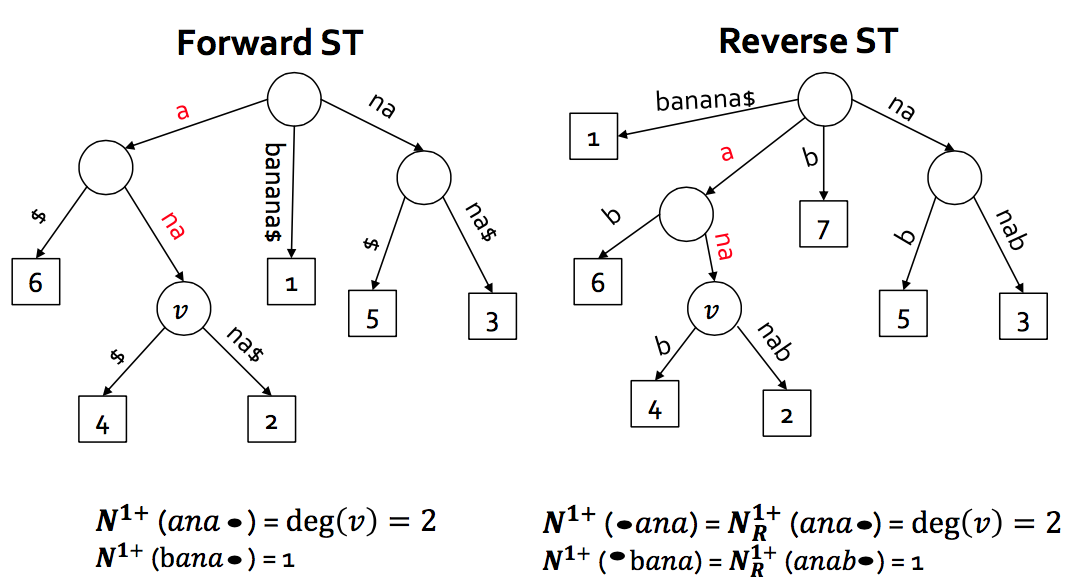
Use 2 CSTs over the text and reverse text

Kneser-Ney Language Modeling

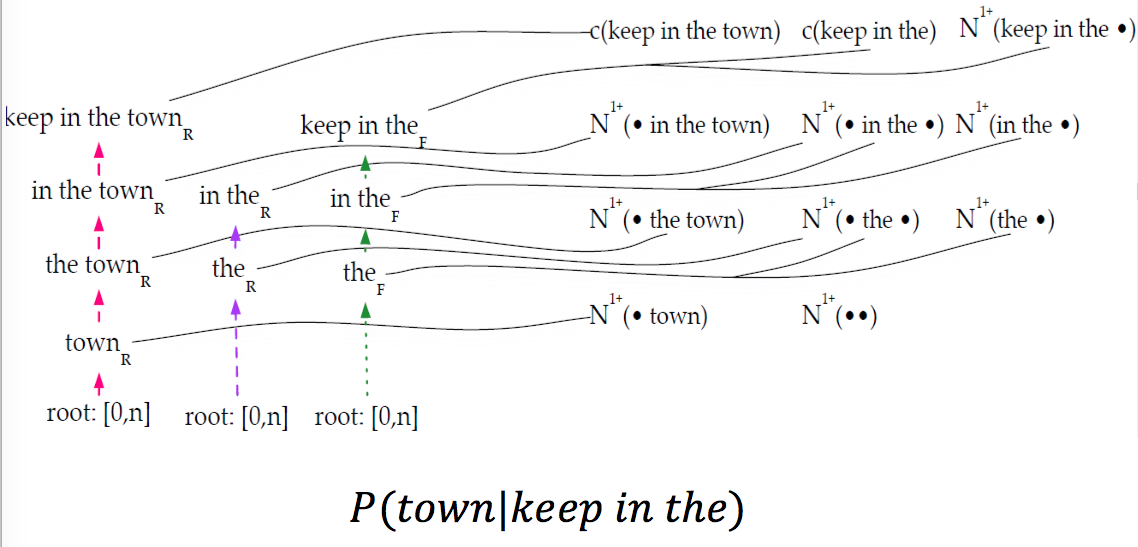
Perform backward search and keep track of dependencies

Computing $N_{1+}(\bullet w_{i}^j \bullet)$

Naive Approach: (Expensive!)

Find the set S of all symbols preceding $w_{i}^j$
For each $\alpha \in S$ determine $N_{1+}(\alpha w_{i}^j \bullet)$
Sum over all $\alpha$

Only use one wavelet tree based CST over the text

$N_{1+}(w_{i}^j \bullet)$ computed as before using the CST
$N_{1+}( \bullet w_{i}^j)$: For the range $[sp,ep]$ of the pattern use the wavelet tree to visit all leaves in $BWT[sp,ep]$. (Interval Symbols in SDSL)
$N_{1+}( \bullet w_{i}^j \bullet )$: Visiting all leaves in $BWT[sp,ep]$ implicitly computes all Weiner Links of the CST node corresponding to $w_{i}^j$ as all [sp,ep] ranges of all $\bullet w_{i}^j$ are computed during the wavelet tree traversal.
Determine number of children of the found nodes to compute $N_{1+}( \bullet w_{i}^j \bullet )$.

Other Considerations

Special case when pattern search ends in the middle of an edge in the CST

Special handling of start and end of sentence tags which can mess up the correct counts

Ensure correctness by comparing to state-of-the-art systems (KenLM and SRILM)

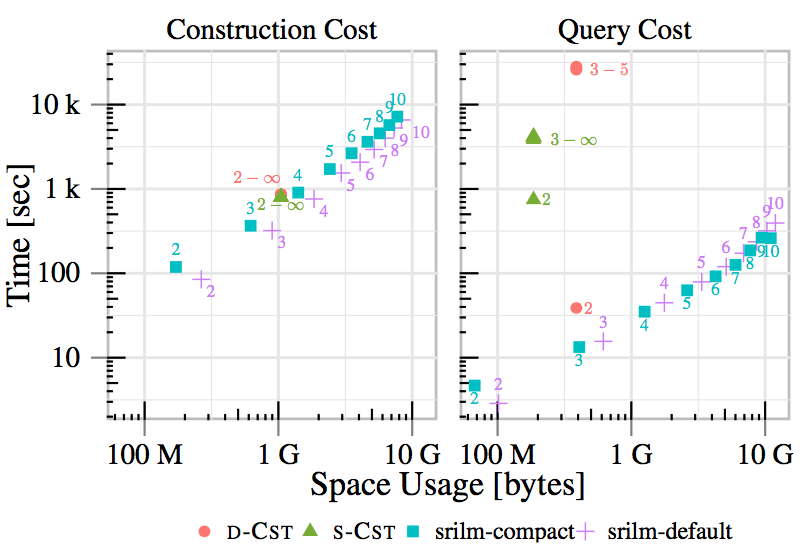
Construction and Query Time

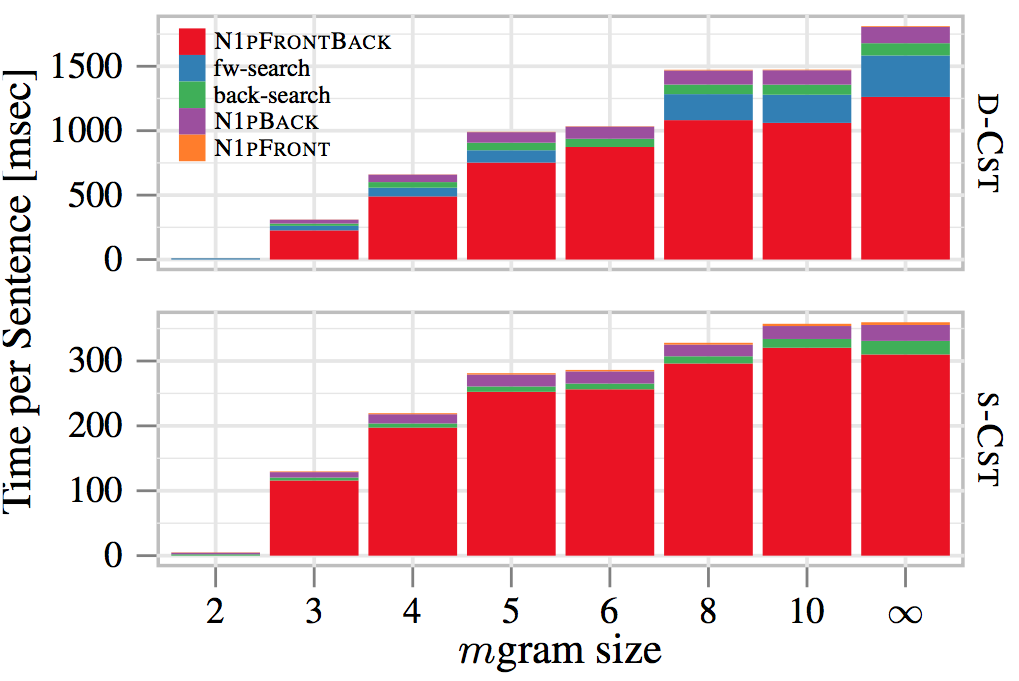
Query Time Breakdown

Future Work

Precomputing some of the counts is very cheap and speeds up query processing significantly
Alphabet-Partitioning for larger alphabets (requires interval symbols)
Already competitive to state-of-the-art implementations
Backward Search now main cost factor
Lots of open problems in the MT field where succinct structures could be applied to
Easy entry as test collections and software are freely available